Computation of ultimate basis sets in realistic body models
Citation

Bastien Guerin, Jorge F Villena, Athanasios G Polimeridis, Elfar Adalsteinsson, Luca Daniel, Jacob White and Lawrence L Wald (2014). "The ultimate SNR and SAR in realistic body models". Annual meeting of the International Society for Magnetic Resonance in Medicine. Milan, Italy.
Bastien Guérin, Jorge F. Villena, Athanasios G. Polimeridis, Elfar Adalsteinsson, Luca Daniel, Jacob K. White, Bruce R. Rosen and Lawrence L. Wald (2016). "Ultimate hyperthermia: Computation of the best achievable radio-frequency hyperthermia treatments in non-uniform body models". Annual meeting of the International Society for Magnetic Resonance in Medicine. Singapore.
What this code does
The code packages linked below are used to compute ultimate basis-set in realistic body models and then use these basis-sets to compute the ultimate SNR. The ultimate basis-set code package contains the Matlab scripts and MARIE routines that are required to compute basis-sets in non-uniform body models as described in the citations above. MARIE is a freely available ultra-fast volume integral solver. You may download it separately or as part of the basis-set package linked below. Downloading the latest version of MARIE will ensure that you are using the fastest/lastest/most bug-free version of the software, however I do not guarantee that it will interface perfectly with the ultimate basis-set scripts. The MARIE routines included in the package linked below may be a bit "old", but they interface with the ultimate basis-scripts without errors. The other code package included below contains Matlab functions to compute the ultimate SNR given a set of basis-set electromagnetic fields in the body model.
Computer requirements
Ultimate basis-set computations are usually long (at least 24 hours for a simple model, a few days for complex models or high frequencies -- see the citations above). Therefore to run this code, I recommend the following computer requirements (these are a not strictly speaking required... You may try the simulation on a slower computer and pray that it works or simply wait longer!!):
- RAM: At least 64 GB
- CPUs: At least 8 cores
- GPU: A GPU is required for this application, which is used to accelerate the main MARIE solve (computational bottleneck of the approach). Although technically speaking MARIE can run without a GPU (the presence of a GPU is detected automatically. The code uses it if on is founds, otherwise multiple CPUs are used), without the GPU computation times may become impractical (e.g. more than 2 weeks basis-sets with 2000 basis vectors and more). I recommend using at least a Tesla K20.
Download files
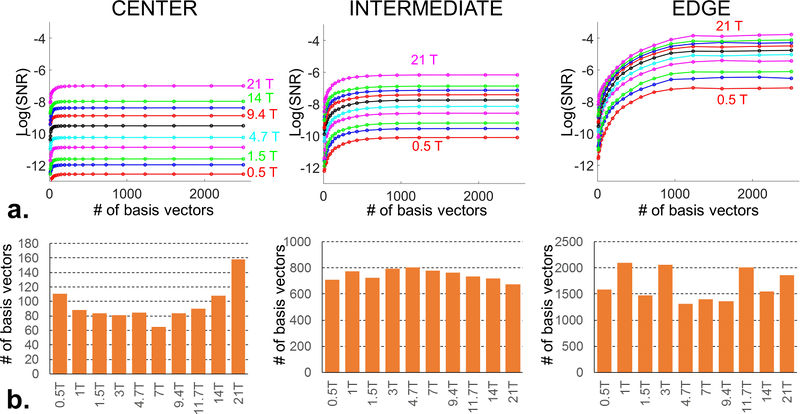
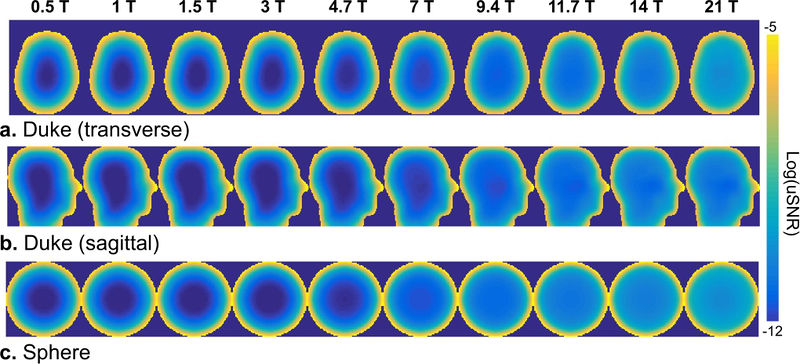
The ultimate basis-set computation code, bundled with MARIE, can be downloaded here. A folder containing the main computation scripts as well as an example body model (Duke @ 7 T, 3 mm isotropic spatial resolution) can be downloaded here. The code required to compute the ultimate SNR from an basis-set of electromagnetic basis fields can be downloaded here. The uSNR and uSENSE results presented in the paper ***UPDATE THIS*** for Duke at field strengths 0.5 T, 1 T, 1.5 T, 3 T, 4.7 T, 7 T, 9.4 T, 11.7 T, 14 T and 21 T can be downloaded here and here (these are Matlab files with self-explanatory directory names and structures).
Instructions for computation of the ultimate basis-set
Main script options
To run an example of ultimate basis-set, download this folder and unzip it. Edit the Matlab script RUN_UBASIS_SCRIPT.m and change the code path to wherever you installed the main ultimate basis-set Matlab package. The options in this script are:
- Frequency expressed in Hz
- Path of the output directory containing all results
- Dmin: The minimum distance between the dipole cloud and the body model in meter
- Dmax: The maximum distance between the dipole cloud and the body model in meter (Dmax-Dmin is the dipole cloud thickness)
- Nexc: Number of random excitations (the total number of basis vectors is 2*Nexc since every random excitation is applied separately to the electric and magnetic dipole clouds)
- tol: Tolerance of the MARIE solver (I recommend leaving this to 1e-8)
- maxit: Maximum iteration of the MARIE solver (I recommend setting this to a large number, e.g. 1e6, to ensure convergence)
This script reads in a body model, in the example provided it is called DUKE_model_3mm_FLOOD_7T.mat. The body model structure should contain the following Matlab arrays:
- COND: Nx*Ny*Nz conductivity array in S/m
- DENS: Nx*Ny*Nz density array in kg/m^3
- PERM: Nx*Ny*Nz relative permittivity array (no unit)
- MASK: Nx*Ny*Nz mask array
- xlim: Position of the X pixels in meter
- ylim: Position of the Y pixels in meter
- zlim: Position of the Z pixels in meter
Note that the Z axis is by definition the B0 direction -- this matters when exporting the B1- and B1+ maps at the end of the calculation.
Computation steps in the main script
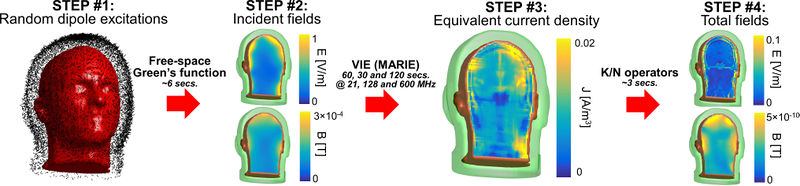
As described in the main script, the computation has 4 main steps:
- ubasis_prepare: In this step, the distance between every "air voxel" located outside the body model and the outer surface of the body is computed. For this calculation to be accurate, make sure that the mask is "flooded", i.e. that internal air voxels corresponding to the sinuses, lungs, mouth etc... are equal to 1 and not 0. Otherwise, you'll end up placing dipoles inside the body model, which is obviously not realistic for most applications. The list of air voxelx-to-body surface distances is saved in the mask_dip2.mat structure.
- ubasis_comp_inc_basis: This function generates the random excitations of the dipole cloud and compute the incident fields corresponding to these random dipole currents.
- ubasis_solve: This function solves the volume polarization current created inside of each non-zero voxel of the body model by the incident fields. This is the main MARIE solve and thus the computational bottleneck of the approach.
- ubasis_comp_fields: This last function computes the total fields, which are the sum of the incident and scattered fields (the latter are obtained from the volume polarization current fields solved in the previous). It also saves the B1- and B1+ maps as well as the loss matrix that is required to compute the ultimate SNR.
Instructions for computation of the ultimate SNR
Once the ultimate basis-set computation is done, you need to dump the various maps and loss matrices in the proper format using the save_data_binary script in the RUN_DUKE_BASIS_SET/ package. Then, simply run the function compute_usnr_unacc_fast_v3 in the unaccelerated_matlab/ folder package to compute the ultimate SNR using this basis-set. The arguments are:
- nx: Number of X voxels of the B1- maps
- ny: Number of Y voxels of the B1- maps
- nz: Number of Z voxels of the B1- maps
- nchannels: Number of basis vectors in the basis set
- datadir: Path of the directory containing the ultimate basis-set
- b1target: B1- target (this is an internal variable using for optimization, the final uSNR result does not depend on it. You can simply set it to 1e-3)
- mask: Mask indicating which pixels the uSNR is computed for.
- lossmatfilepref: Prefix of the loss matrix.
If anything is not clear, simply look at the code -- it should be pretty straightforward to understand!